Шведская компания AmpTrack Technologies AB объявила о запуске на российском рынке своей онлайн-DAW Amped Studio 2.2. Онлайновая программа для записи музыки и студия звукозаписи работает прямо в окне браузера и предоставляет аналогичный десктопным и офлайновым DAW опыт. Пользователи могут создавать музыкальные композиции с аудио и MIDI-треками, как если бы они использовали любую другую, более традиционную программу для записи и создания музыки.
Особую ценность студия представляет для молодых музыкантов, которые только берутся за создание музыки. Привычные настольные программы для записи музыки стоят немалых денег и требуют дорогостоящего оборудования. В отличие от них, Amped Studio упрощает доступ к музыке — для работы нужен только компьютер с доступом в Интернет.
Amped Studio 2.2 оснащается совершенно новой технологией определения тональностей и звуков ударных инструментов Hum And Beatz. Пользователи могут напеть мелодию в микрофон, а Amped Studio автоматически создаст MIDI-ноты и ритмы в проекте. Благодаря этому сочинять музыку можно своим голосом: достаточно выбрать инструмент, напеть партию или пропеть ритм в стиле битбокса, чтобы получить заполненные информацией дорожки.
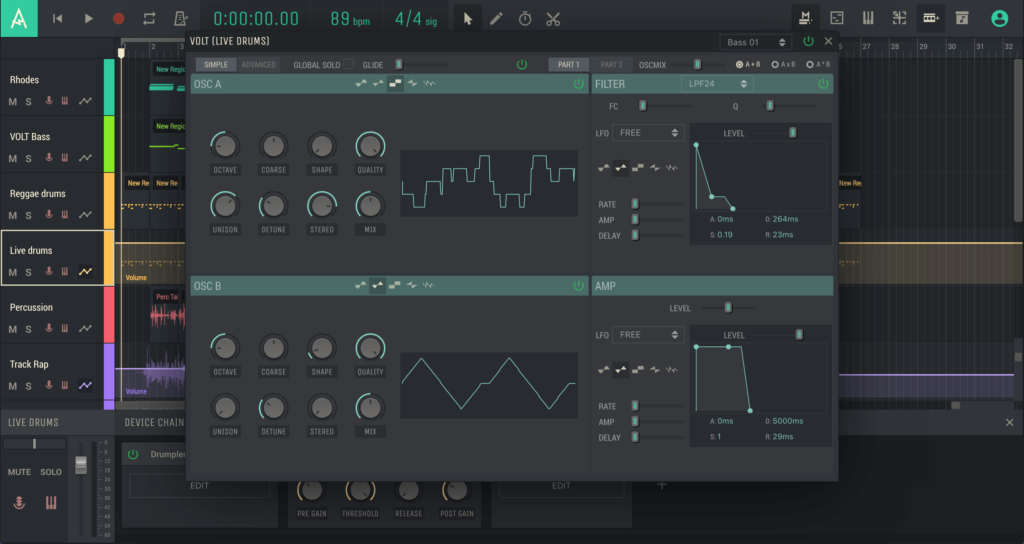
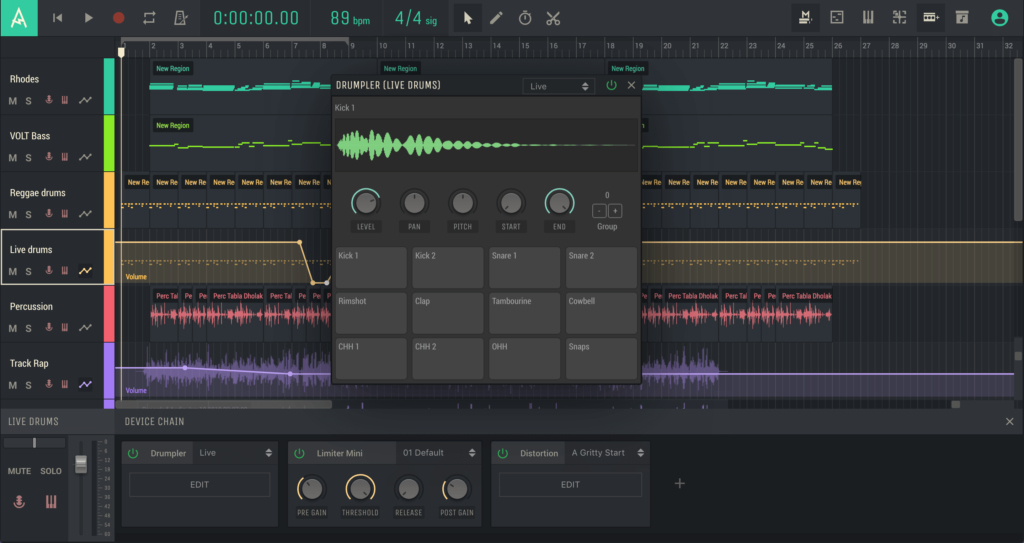
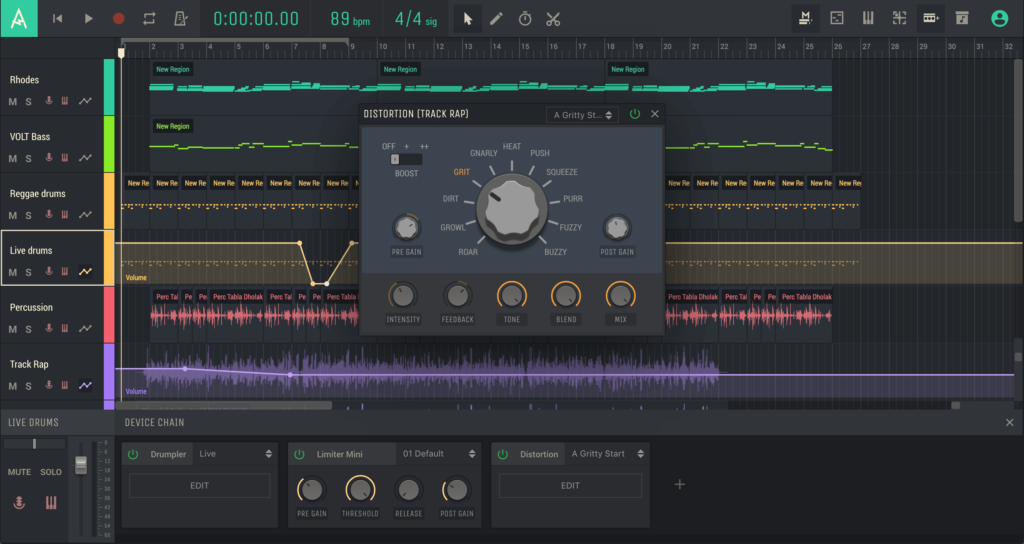
Онлайн-DAW отличается от большинства подобных программ возможностью одновременной записи и воспроизведения аудио и MIDI в рамках одной дорожки. Более того, количество виртуальных инструментов и эффектов ничем не ограничено — в проект можно добавить столько контента, сколько захочется. Благодаря последним обновлениям Amped Studio представляет собой интуитивно понятную и вдохновляющую программу, в состав которой входят эффекты, синтезаторы, инструменты, фильтры, большая коллекция лупов и сэмплов.
По словам генерального директора AmpTrack Technologies AB Била Брайанта, обновление 2.2 выводит производство музыки в онлайне на совершенно новый уровень. «Наряду с добавлением сложных, и в то же время забавных инструментов, мы изучили лучшие функции традиционных программ для создания музыки и перенесли их в Интернет», — говорит Брайант. — «Благодаря нашим технологиям с открытым исходным кодом WAM, многие разработчики плагинов уже конвертируют свои разработки из формата VST в совместимый с Amped Studio формат, чтобы пользователи DAW могли наслаждаться своими любимыми инструментами, где бы они не находились».
Amped Studio 2.2 доступна для использования бесплатно: начальная подписка включает базовые инструменты и функции. Премиальная версия подписки за $4,99 даёт больше инструментов и расширенную библиотеку звуков. Для получения дополнительной информации о выходе русской версии Amped Studio 2.2 стоит посетить страницу https://ampedstudio.com/#ru.

Главное не загнутся раньше времени. Через 10 лет примерно, всё это будет обыденностью и по сути победой над пиратством.
Как по мне онлайн DAW это изврат, слишком много зависимостей. На вопрос зачем, я тоже для себя ответа не тоже нашел, преимуществ тоже не увидел. Типа того что не дорого, сомнительный довод. Так баловство.
Все ж с малого начинается может быть когда нибудь мы все переедем в онлайн и будем думать, что работать на столе в проге уже не тру
но это будет не сегодня явно хD
Ну так её никто не рассматривает как основную… Ну как вариант эту DAW можно использовать для наброска идей не на рабочем месте и возможно не на своем ПК
Разнообразие это всегда хорошо, пусть будет.
Список плагинов, которые можно испольовать в этой DAW, ограничен? Как можно загрузить в эту DAW сторонние плагины?
Как я понял, обычные VST туда не подгрузишь, нужен какой-то конвертер, который превратит их в совместимый софт.
Да, обычные VST не поддерживаются. Хотя это технически возможно, но это бы потребовало установки дополнительного модуля на компьютер пользователя, так же как и самих плагинов, нивелируя преимущества онлайн-платформы. Поэтому мы разработали альтернативный формат для онлайн плагинов WAM.
На данном этапе (помимо встроенных инструментов и эффектов) доступно только два бесплатных синтезатора в качестве демонстрации возможностей технологии и ещё один может быть докуплен на сайте wam.fm
Несколько разработчиков плагинов заинтересовались технологией и портируют свои плагины в настоящее время, но потребуется время пока они станут доступны внутри нашей онлайн-DAW.
Reaper стоит чуть меньше 4 тысяч, Cakewalk by BandLab вообще бесплатный. Не таких уж и больших денег.
А какое именно дорогостоящее оборудование требуют классические DAW? Компьютер? Не понимаю.
Это вопрос к разработчикам, попросили их присоединиться к обсуждению, чтобы дать вам ответ. Мы только опубликовали полученный пресс-релиз, пометив публикацию соответствующим тегом)
В Reaper на сколько я знаю нет инструментов, только обработки. Cakewalk by BandLab только Win.
Surge, Dexed, Obxd, Pg-8x, Synth1, этого бесплатного стаффа уже выше головы