Музыканты играющие на струнных инструментах обычно воспринимают обертона как способ настройки инструментов: к примеру, флажолет/обертон на пятом ладу любой струны гитары звучит так же, как и флажолет на 12 ладу следующей струны. Помимо этого, обертона воспринимаются как более приятный и легкий звук, который можно извлечь. В принципе, большинству таких знаний об обертонах достаточно.
Несмотря на это, обертона обладают огромным потенциалом с точки зрения композиционного инструмента. Вплетенные в исполнение, эти легкие звуки можно использовать в качестве текстур, которые накладываются поверх или поддерживают мелодии и обогащают общее звучание произведения. Просто послушайте, как ловко в своем творчестве обертонами пользовался легендарный басист Жако Пасториус, чтобы понять, о чем речь.
https://www.youtube.com/watch?v=LEs5sKDXZuk
Давайте разберемся, что такое обертон, как он образуется и чем связан с гармониками.
Что такое обертон
Любой звук — это вибрация, колебания объекта в пространстве и времени. Чтобы проще усвоить это, достаточно посмотреть на поведение струны (гитары, баса, скрипки, виолончели), которая начинает колебаться от прикосновения пальца. Постоянно двигаясь вверх и вниз, струна создает колебания, которые мы слышим, и чем чаще амплитуда движений струны, тем громче итоговый звук.

Частота вибрации струны зависит от множества факторов: силы натяжения, материала струн и даже ее длины. Последнее особенно важно, так как изменение длины струны в большую или меньшую сторону меняет характер звука и извлекает звуки, которые называются обертонами (гармониками).
Обертон (от нем. ober — высокий, ton — звук) — это призвук самого звука, звучащий выше него в определенное количество раз (кратное целым числам). Каждый звук имеет собственные обертоны, звучащие на определенной частоте.
Услышать обертон на гитаре или скрипке можно, если извлечь флажолет — поместить палец над струной (не зажать, а слегка прикоснуться к струне) и дернуть ее. Гитаристы знают, что самые яркие флажолеты извлекаются на 12, 7 и 5 ладу, но с точки зрения теории извлекать их можно в любом месте грифа.
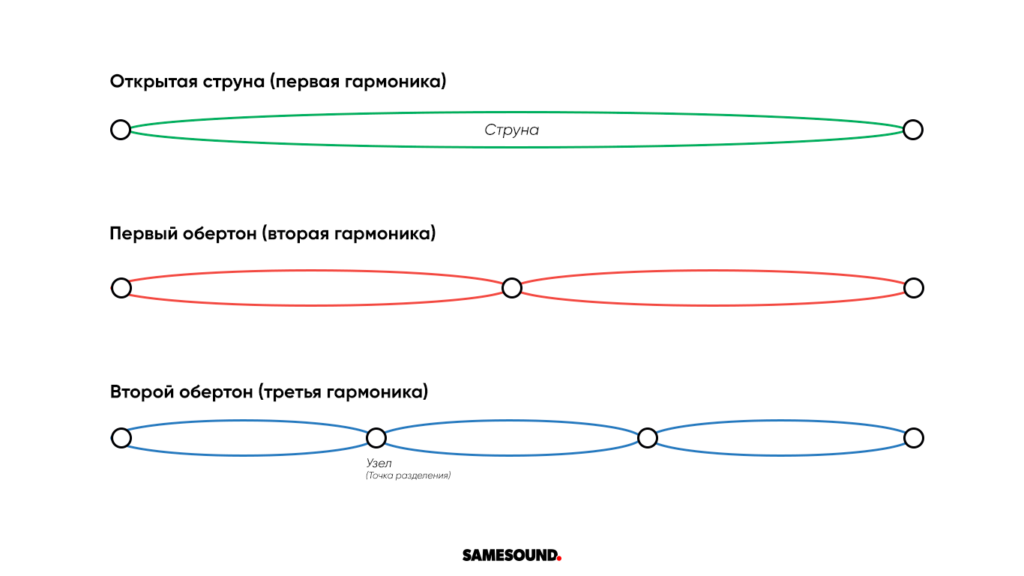
Место, где мы прикасаемся к струне называется узлом, точкой разделения струны, разбивающей ее на математически равные части. Каждый узел сокращает длину струны в определенное количество раз и создает новые обертона и гармоники.
Колебания струны происходят вверх и вниз по всей ее длине и форма звуковой волны в таком случае достаточно проста. Когда мы делим струну на равные части, мы усложняем форму волны — струна начинает колебаться в нескольких местах сразу. При этом колебания двух отрезков всегда происходят в противоположные стороны: если до узла струна движется вверх, то после узла — вниз, и наоборот.
Как найти обертон звука
Итак, мы узнали, что такое обертон, являющийся узлом деления струны с интересным звучанием. То место, где происходит деление (узел, где мы прикасаемся пальцем) и есть точка, в которой появляется обертон. Каждая новая часть струны колеблется самостоятельно, но в гармонии с другими частями, поэтому каждый такой отрезок колебаний называется гармоникой.

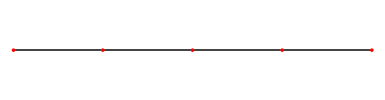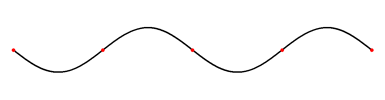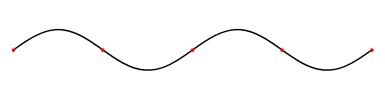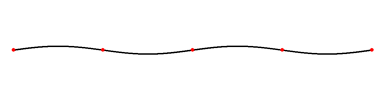
Возьмем пятую струну гитары, настроенную на ноту Ля (стандартный строй). Струна колеблется на частоте 110 Гц (нота Ля), а ее длина составляет примерно 64,8 см (25,5 дюймов). Открытая струна является первой гармоникой, нулевым обертоном.
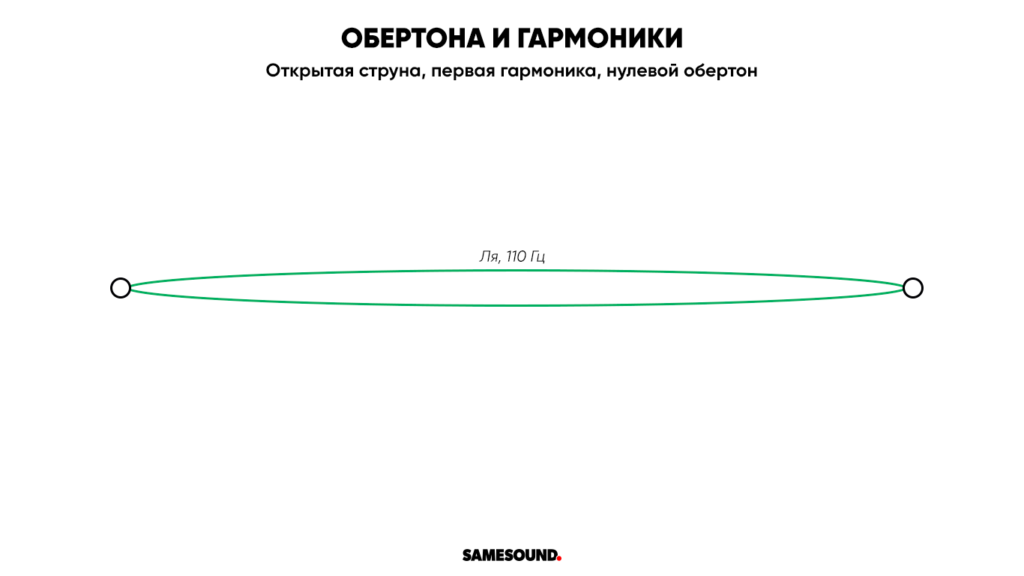
Если мы поместим палец ровно в центре струны, на отметке 32,4 см (12,75 дюймов), то мы сократим ее длину вдвое, а также вдвое увеличим скорость колебаний — до 220 Гц. Увеличенная вдвое скорость колебаний приведет к образованию звука выше на октаву: первый обертон для Ля (открытая пятая струна) будет находиться на 12 ладу и звучать как Ля на октаву выше.
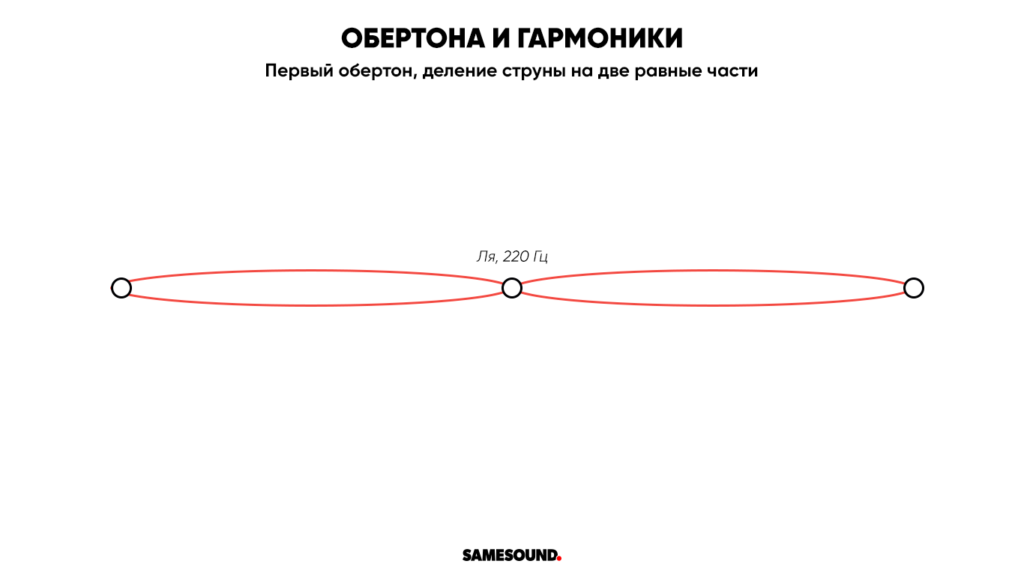
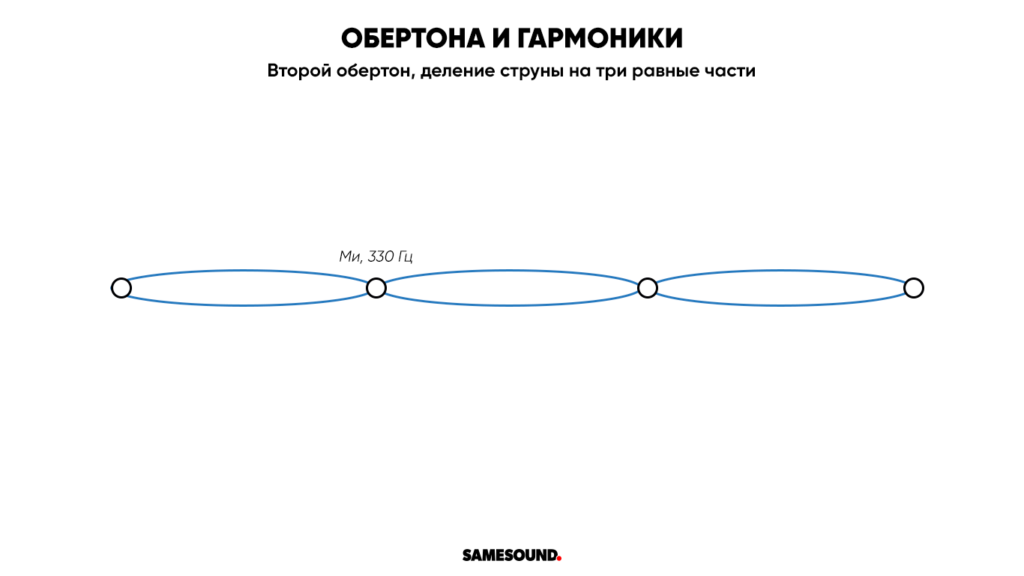
Разделив струну на три равные части и поместив палец на конце трети (на седьмом ладу, 21,6 см от верхнего порожка, соотношение 1:3), мы искусственно укоротим струну втрое и повысим частоту колебаний до 330 Гц. Второй обертон в нашем случае произведет звук выше на октаву и квинту — на седьмом ладу мы услышим Ми.
Начиная с этого момента, мы можем и дальше делить струну на равные части и находить другие обертона:
- Соотношение 1:4 позволит найти третий обертон (на пятом ладу). Извлекаемый звук будет звучать на две октавы выше от исходного тона;
- Соотношение 1:5 — четвертый обертон, звук на две октавы и большую терцию выше исходного. На гитаре четвертый обертон будет располагаться в самом начале 4 лада;
- Соотношение 1:6 поделит струну на шесть равных частей (шесть гармоник). Пятый обертон звучит на две октавы и чистую квинту выше основного тона и на гитаре находится прямо в конце третьего лада.
Что делать с обертонами и гармониками?
Что такое обертон для музыканта? Правильно, еще один инструмент для самовыражения и украшения своих партий. К примеру, гитарист может обогатить соло с помощью своеобразных визжащих призвуков, которые часто становятся неожиданностью для слушателя и лучше врезаются в память.
Помимо этого, гармоники можно вплетать в гитарные риффы, эффектно завершая гармоническими визжащими звуками концы квадратов или фраз.
https://youtu.be/XjDS56870cs?t=3m17s
Удачи в творчестве!